An Assignment of Probability Must Obey Which of the Following

By fu_Cierra467 10 May, 2022 Post a Comment

Which of the following must be true. An assignment of probabilities must obey which of the following.

Solved An Assignment Of Probabilities Events Sample Space Must Obey Which Of The Following The Probability Of Any Event Must Be Number Betwcen And Inclusive They Must Sum To When Adding Over All

P A U B U C P A P B P C P S 1.

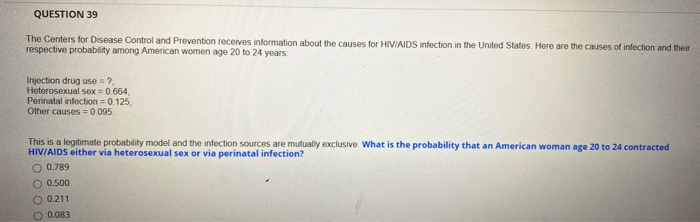
. A third event C has probability 06. A and B only. Are disjoint events then P E 1 E 2 E 3 X1 i1 P E i Theorem.

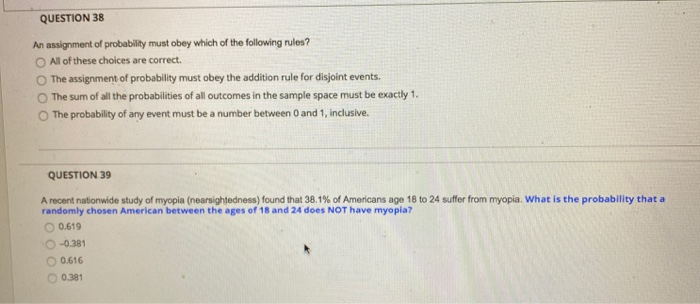
COUNTING AND PROBABILITY Axioms of Probability. C The probability of an event is the sum of the outcomes in the sample space which make up the event. A the probability of any event must be a number between 0 and 1 inclusive B the sum of all the probabilities of all outcomes in the sample space must be exactly 1 C it must obey the addition rule for disjoint events D all of the above.

They must sum to I when adding over all events in the sample space. Event B has probability 05. I flip a coin twice and count the.

A The probability of any event must be a number between 0 and 1 inclusive. Apart from the stuff given above if you need any other stuff in math please use our. The sum of all the probabilities of all outcomes in the sample space must be exactly 1.

C The probability of an event is the sum of the outcomes in the sample space which make up the event. B The sum of all the probabilities of all outcomes in the sample space must be exactly 1. An assignment of probability must obey which of the following.

An assignment of probability must obey which of the following. B The sum of the probabilities of all outcomes in the sample space must be exactly 1. Are disjoint events then PE 1 E 2 E 3 X1 i1 PE i Theorem Basic theorems of probability.

B The sum of the probabilities of all outcomes in the sample space must be exactly 1. An event is a set of outcomes. D Il of the above.

The probability of any event must be a number between 0 and 1 inclusive. C must have some elements in common with at least one of A or B. Up to 24 cash back 1.

A The probability of any event must be numbered between 0 and 1 inclusive. An assignment of probability must obey which of the following. Where the weights wn from the spectral decomposition of W sum to 1.

A The probability of any event must be a number between 0 and 1 inclusive. An assignment of probability must obey which of the following. E A and B only.

B The sum of all the probabilities of all outcomes in the sample space must be exactly 1. All of these choices are correct. C The probability of an event is the sum of the outcomes in the sample space that make up the event.

1 P 0. C The probability of an event is the sum of the outcomes in the sample space that make up the event. D All of the.

The assignment of probabilities to events must obey the following rules. So by axioms of probability. The probability of either a Junior or Senior will be 1 - P Freshman or Sophomore 1 - 3530 1 - 65 35 or 35 B.

20 An assignment of probability must obey which of the following. A The probability of any event must be a number between 0 and 1 inclusive. A The probability of any event must be a number between 0 and 1 inclusive.

An assignment of probability must obey which of the following. If the number of spots showing is either four or five you win 1. The probability of any event must be a number between 0 and 1 inclusive.

Let Aand Bbe events. A The probability of any event must be a number between 0 and 1 inclusive. So the assignment of probability is permissible.

B The sum of all the probabilities of all outcomes in the sample space must be exactly 1. D All of the above. Let W be a state that assigns probability 1 to one-dimensional Q.

22 Tr W Q n w n e n Q e n 1. The probability of any event must be a number between 0 and l inclusive. The sum of all the probabilities of all outcomes in the sample space must be exactly 1.

O The sum of all the probabilities of all outcomes in the sample space must be exactly 1. All of the above 25. B The sum of all the probabilities of all outcomes in the sample space must be exactly 1.

If S is a sample space consisting of N equally likely outcomes and E is an event consisting. D All of the above. C The probability of an event is the sum of the outcomes in the sample space which make up the event.

The probability of any event must be a number between 0 and 1 inclusive. A The probability of any event must be a number between 0 and 1 inclusive. 1 PE 0 for any event E 2 PS 1 3 If E 1E 2E 3.

In a particular game a fair die is tossed. The sum of all the probabilities of all outcomes in the sample space must be exactly 1. All of these choices are correct.

An assignment of probability must obey which of the following. The probability of any event must be a number between 0 and 1 inclusive. The probability of any event must be a number between 0 and 1 inclusive.

A The probability of any event must be numbered between 0 and 1 inclusive. An assignment of probability must obey which of the following. They must obey the addition rule for disjoint events.

All of the. 13 1 - 13 0. An assignment of probability must obey which of the following.

The assignment of probability must obey the addition rule for disjoint events. It must obey the addition rule for disjoint events. The assignment of probability to events in a sample space S must obey the following rules.

An assignment of probabilities must obey which of the following. 1 PE 0 for any event E 2 PS 1 3 If E 1E 2E 3. The sum of all the probabilities of all outcomes in the sample space must be exactly 1.

The probability of an event is the sum of the outcomes in the sample space which make up the event. B The sum of all the probabilities of all outcomes in the sample space must be exactly 1. P A 0 P B 0 and P C 0.

An assignment of probabilities to events in a sample space must obey which of the following. The assignment of probability must obey the addition rule for disjoint events. The probability of an event is the sum of the outcomes in the sample space which make up the event.

B The sum of all the probabilities of all outcomes in the sample space must be exactly 1. Probability of an event can be 1. Introducing Probability 59 13.

Writing W in terms of its spectral decomposition and taking the trace in a basis determined by W we immediately find that.

Solved Question 38 An Assignment Of Probability Must Obey Chegg Com